How To Find Parallel And Perpendicular Components Of A Vector

Vectors in Two and Iii Dimensions

Part 6: Projections

Use the applet beneath to investigate the projection of a vector v (green) onto some other vector w (yellow ) in infinite, which we volition relate before long to the dot product <v,west>. Y'all can adjust the components of the yellowish and green vectors and and so ask the applet to compute the projection of the green vector onto the yellow. The slider at the lesser allows you lot to rotate the view of the vectors. To help keep you oriented, the projections of the dark-green and yellowish vectors onto the xy-aeroplane are also shown. The projection of a vector five onto w is a vector in the same or opposite management as due west, and then there are two things to exist determined: "same or opposite" and the length of the projection. Think about how both of these might exist related to the dot product.

We volition use the idea of projecting one vector onto some other to resolve a vector 5 into its components parallel and perpendicular to a vector w. The idea is illustrated in the following figure, which is fatigued in the aeroplane determined by v and west.

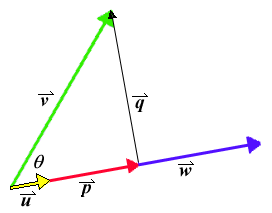
In this effigy, v is shown in green and due west in blue (partly obscured by u and p). The vector p is the projection of v on w, and this is also the component of v parallel to westward. The component of v perpendicular to w is q, and clearly v = p + q. Thus, if nosotros can notice p from five and westward, so nosotros tin summate q every bit q = v - p.

For purposes of indicating the direction of w, nosotros starting time calculate a unit vector u (i.e., u has length one) in the aforementioned direction as u. How is u calculated from w? Explain why p = |p| u. How is |p| related to the length of v and the cosine of the bending between them?
Observe that cos can be calculated by taking the dot product of 5 with either of the vectors w or u. (We can't utilize p for this purpose considering we don't know what it is still -- that 'due south what we're trying to detect.) Now put all the pieces together to arrive at a formula for p past finding u, cos , |p|, and finally p itself.
Acquit out your formula to find the projection of five = (two,1,iii) onto due west = (two,four,2). Then find both the parallel and perpendicular components of v relative to west. If your calculation is correct, the two components should be perpendicular -- cheque that.
Utilise your formula for p to show that p and five - p are always perpendicular.