How To Find The Area Of An Isosceles Triangle

The area of an isosceles triangle is the corporeality of region enclosed past it in a two-dimensional space. The general formula for the area of triangle is equal to half the product of the base and top of the triangle. Here, a detailed explanation near the isosceles triangle area, its formula and derivation are given along with a few solved example questions to make it easier to take a deeper understanding of this concept.

Cheque more than mathematics formulas here.

What is the Formula for Area of Isosceles Triangle?

The total surface area covered past an isosceles triangle is known as its area. For an isosceles triangle, the area can exist hands calculated if the pinnacle (i.e. the distance) and the base are known. Multiplying the superlative with the base and dividing it past 2, results in the area of the isosceles triangle.

What is an isosceles triangle?

An isosceles triangle is one that has at least two sides of equal length. This belongings is equivalent to ii angles of the triangle being equal. An isosceles triangle has two equal sides and two equal angles. The proper noun derives from the Greek iso (same) and Skelos (leg). An equilateral triangle is a special case of the isosceles triangle, where all the three sides and angles of the triangle are equal.

An isosceles triangle has two equal side lengths and two equal angles, the corners at which these sides run into the third side is symmetrical in shape. If a perpendicular line is drawn from the bespeak of intersection of two equal sides to the base of the diff side, so two right-angle triangles are generated.

Expanse of Isosceles Triangle Formula

The area of an isosceles triangle is given by the following formula:

Also,

The perimeter of the isosceles triangle	P = 2a + b
The altitude of the isosceles triangle	h = √(a2 − b2/4)

Listing of Formulas to Find Isosceles Triangle Surface area

Formulas to Observe Area of Isosceles Triangle
Using base and Height	A = ½ × b × h
Using all three sides	A = ½[√(a2 − b2 ⁄4) × b]
Using the length of ii sides and an angle between them	A = ½ × b × c × sin(α)
Using 2 angles and length betwixt them	A = [c2×sin(β)×sin(α)/ 2×sin(2π−α−β)]
Area formula for an isosceles right triangle	A = ½ × aii

How to Calculate Expanse if Just Sides of an Isosceles Triangle are Known?

If the length of the equal sides and the length of the base of an isosceles triangle are known, so the height or altitude of the triangle is to be calculated using the post-obit formula:

The Altitude of an Isosceles Triangle = √(a² − b^two/4)

Thus,

Area of Isosceles Triangle Using Only Sides = ½[√(a² − b² /four) × b]

Here,

• b = base of the isosceles triangle
• h = height of the isosceles triangle
• a = length of the 2 equal sides

Derivation for Isosceles Triangle Area Using Heron's Formula

The expanse of an isosceles triangle can be easily derived using Heron'due south formula as explained beneath.

According to Heron'due south formula,

Area = √[southward(s−a)(s−b)(southward−c)]

Where, s = ½(a + b + c)

Now, for an isosceles triangle,

s = ½(a + a + b)

⇒ s = ½(2a + b)

Or, due south = a + (b/two)

Now,

Area = √[south(s−a)(south−b)(southward−c)]

Or, Area = √[s (south−a)ⁱⁱ (s−b)]

⇒ Area = (due south−a)× √[s (s−b)]

Substituting the value of "s"

⇒ Area = (a + b/ii − a)× √[(a + b/2) × ((a + b/2) − b)]

⇒ Area = b/2 × √[(a + b/2) × (a − b/2)]

Or, area of isosceles triangle = b/2 × √(a² − bⁱⁱ/4)

Area of Isosceles Correct Triangle Formula

The formula for Isosceles Right Triangle Area= ½ × a²

Derivation:

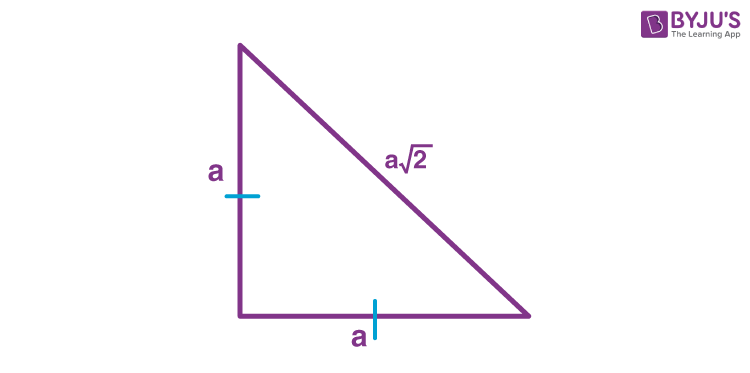
Expanse = ½ ×base × tiptop

surface area = ½ × a × a = a²/2

Perimeter of Isosceles Right Triangle Formula

Derivation:

The perimeter of an isosceles right triangle is the sum of all the sides of an isosceles right triangle.

Suppose the 2 equal sides are a. Using Pythagoras theorem the unequal side is found to be a√ii.

Hence, perimeter of isosceles right triangle = a+a+a√two

= 2a+a√2

= a(2+√ii)

= a(2+√ii)

Area of Isosceles Triangle Using Trigonometry

Using Length of 2 Sides and Angle Between Them

A = ½ × b × c × sin(α)

Using 2 Angles and Length Between Them

A = [c^two×sin(β)×sin(α)/ 2×sin(2π−α−β)]

Example Questions

Question 1: Find the area of an isosceles triangle given b = 12 cm and h = 17 cm?
Solution:

Base of the triangle (b) = 12 cm

Height of the triangle (h) = 17 cm

Area of Isosceles Triangle = (1/2) × b × h

= (ane/2) × 12 × 17

= half dozen × 17

= 102 cm²

Question 2: Find the length of the base of an isosceles triangle whose area is 243 cm^ii, and the altitude of the triangle is 27 cm.

Solution:

Area of the triangle = A = 243 cm^two

Height of the triangle (h) = 27 cm

The base of operations of the triangle = b =?

Expanse of Isosceles Triangle = (1/ii) × b × h

243 = (1/2) × b × 27

243 = (b×27)/2

b = (243×2)/27

b = 18 cm

Thus, the base of the triangle is 18 cm.

Question iii: Detect the surface area, distance and perimeter of an isosceles triangle given a = 5 cm (length of two equal sides), b = 9 cm (base of operations).

Solution:

Given, a = 5 cm

b = nine cm

Perimeter of an isosceles triangle

= 2a + b

= 2(five) + 9 cm

= 10 + 9 cm

= xix cm

Altitude of an isosceles triangle

h = √(a² − b²/iv)

= √(v² − 9²/4)

= √(25 − 81/4) cm

= √(25–81/iv) cm

= √(25−20.25) cm

= √4.75 cm

h = 2.179 cm

Area of an isosceles triangle

= (b×h)/two

= (9×2.179)/2 cm²

= xix.611/2 cm²

A = nine.81 cm²

Question four: Find the area, altitude and perimeter of an isosceles triangle given a = 12 cm, b = 7 cm.

Solution:

Given,

a = 12 cm

b = seven cm

Perimeter of an isosceles triangle

= 2a + b

= 2(12) + seven cm

= 24 + 7 cm

P = 31 cm

Altitude of an isosceles triangle

= √(a² − b^two⁄iv)

= √(12ⁱⁱ−7^two/four) cm

= √(144−49/4) cm

= √(144−12.25) cm

= √131.75 cm

h = eleven.478 cm

Area of an isosceles triangle

= (b×h)/two

= (7×11.478)/2 cm²

= 80.346/two cm²

= forty.173 cm²

Frequently Asked Questions

What is an Isosceles Triangle?

An isosceles triangle tin be divers every bit a special type of triangle whose 2 sides are equal in measure. For an isosceles triangle, forth with two sides, two angles are also equal in measure.

What does the Area of an Isosceles Triangle Mean?

The expanse of an isosceles triangle is defined as the amount of space occupied by the isosceles triangle in the two-dimensional plane.

What is the Formula for Area of Isosceles Triangle?

To calculate the area of an equilateral triangle, the following formula is used:

A = ½ × b × h

What is the Formula for Perimeter of Isosceles Triangle?

The formula to calculate the perimeter of an equilateral triangle is:

P = 2a + b

Source: https://byjus.com/maths/area-of-isosceles-triangle/

Posted by: padillatront1952.blogspot.com

Share this post